Non-adiabatic dynamics
Developing mixed-quantum classical methods for complex-valued Hamiltonians.
The Fewest-Switches Surface Hopping (FSSH) algorithm is one of the most popular approaches for simulating non-adiabatic dynamics, where one propagates classical trajectories on a single electronic energy surface and integrates the electronic Schrodinger equation for each trajectory. Trajectories are allowed hop to other surfaces stochastically based on their associated quantum amplitudes.
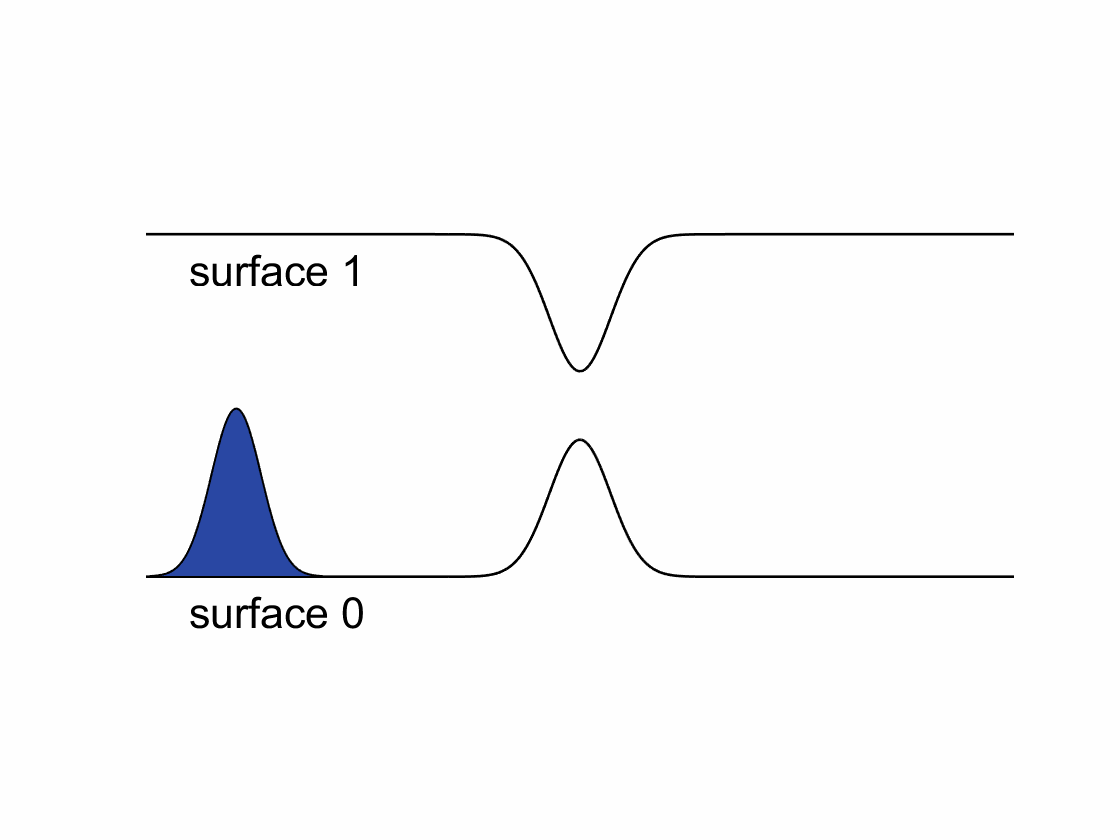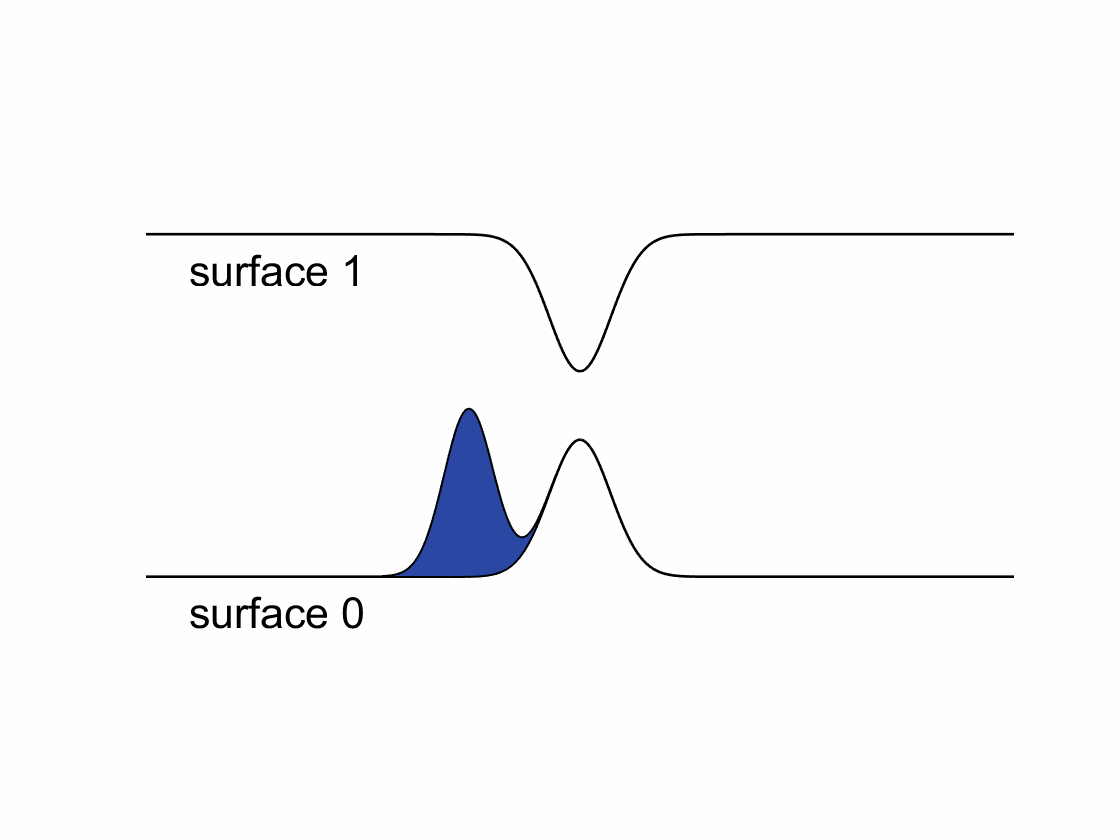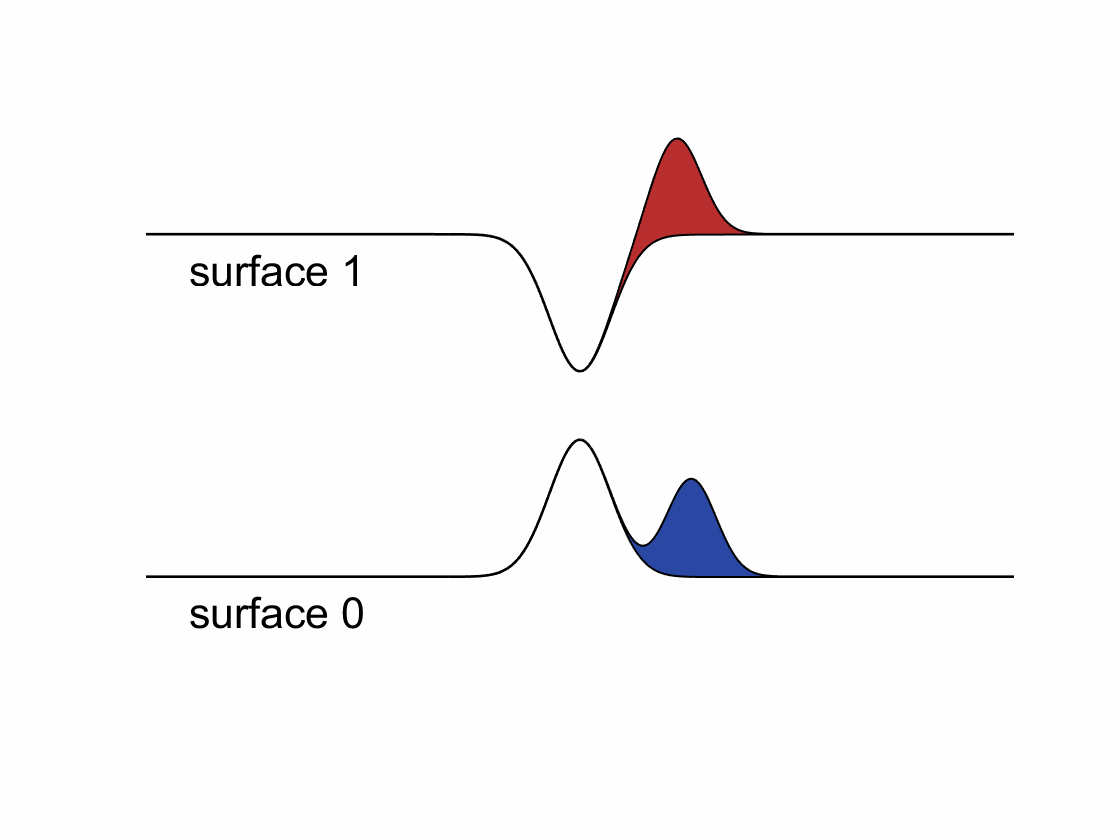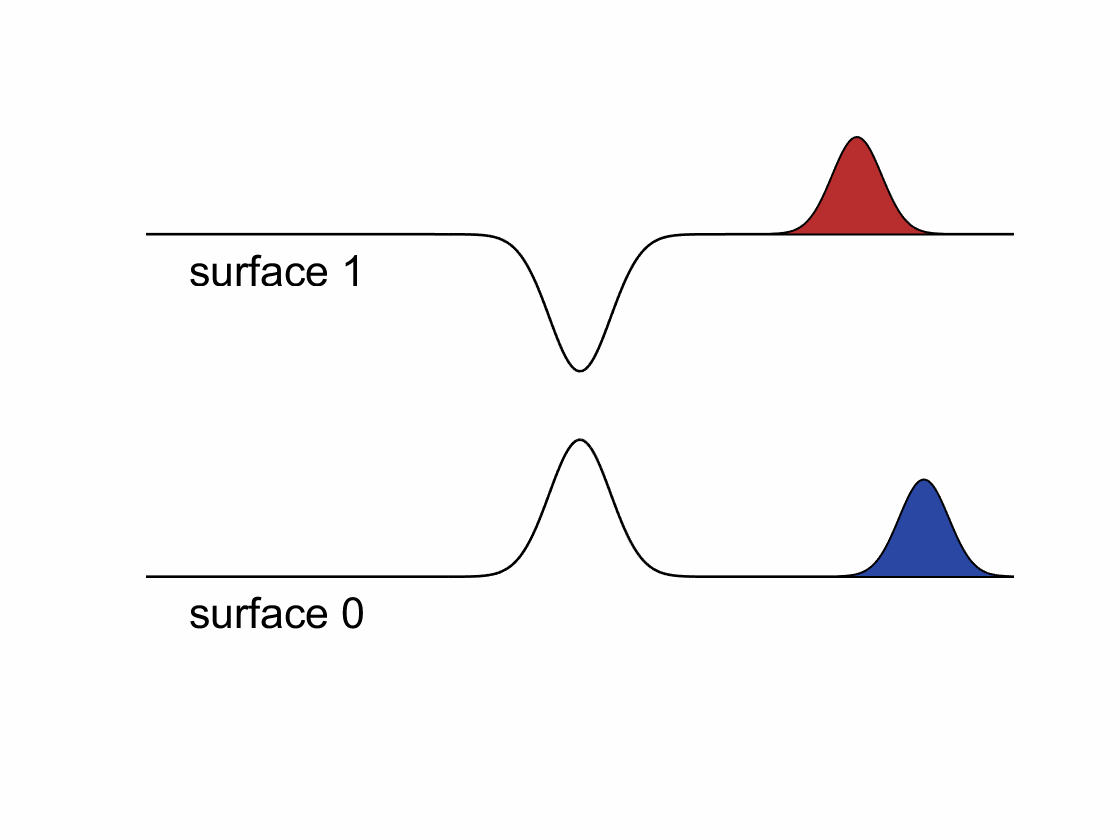
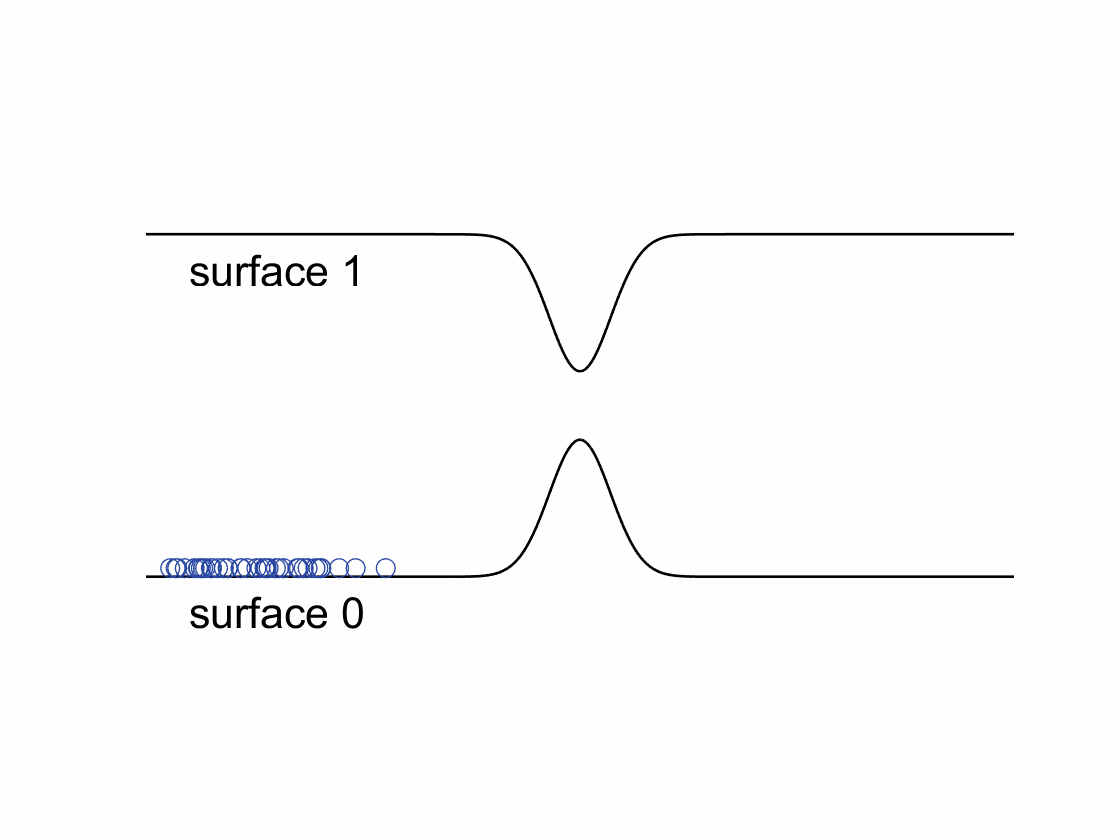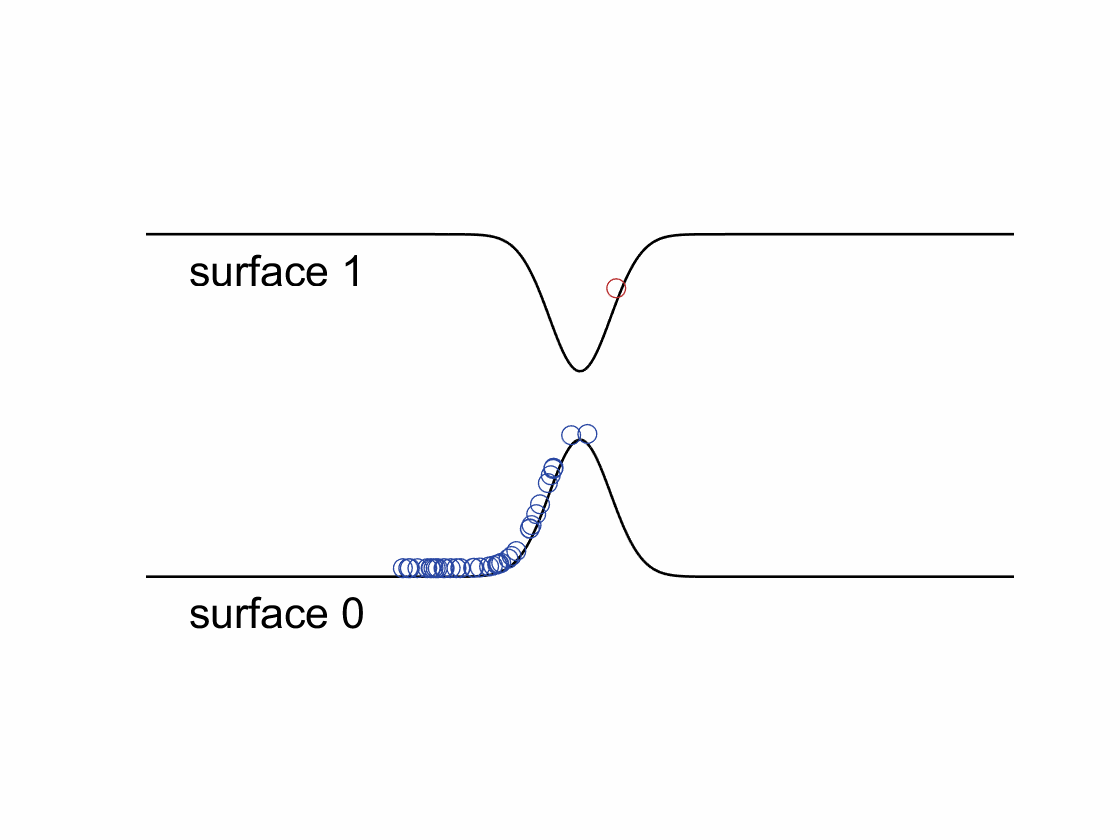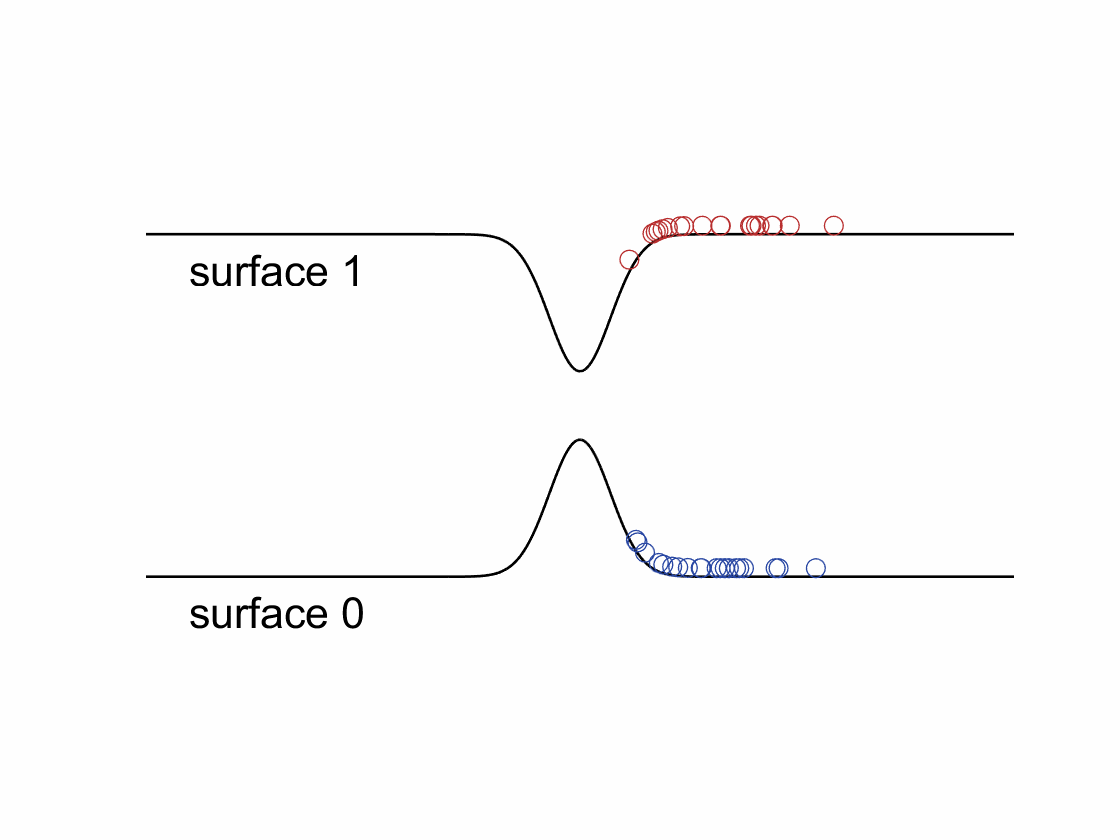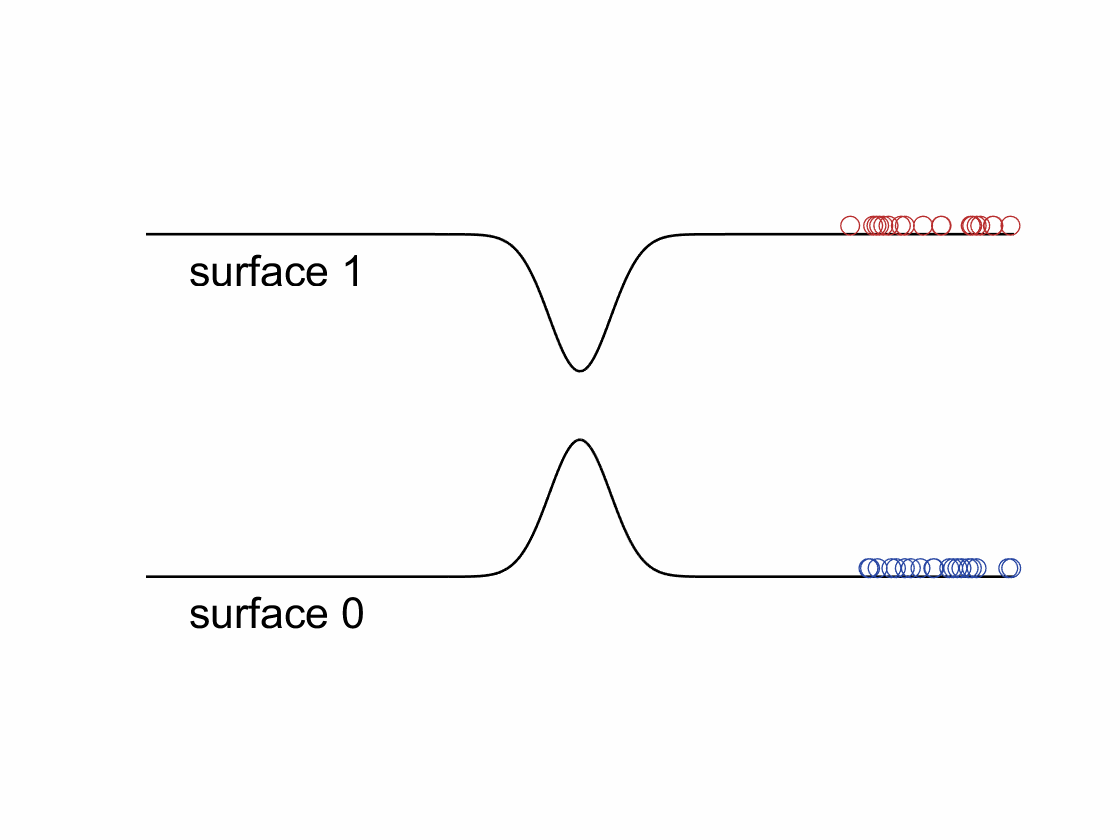
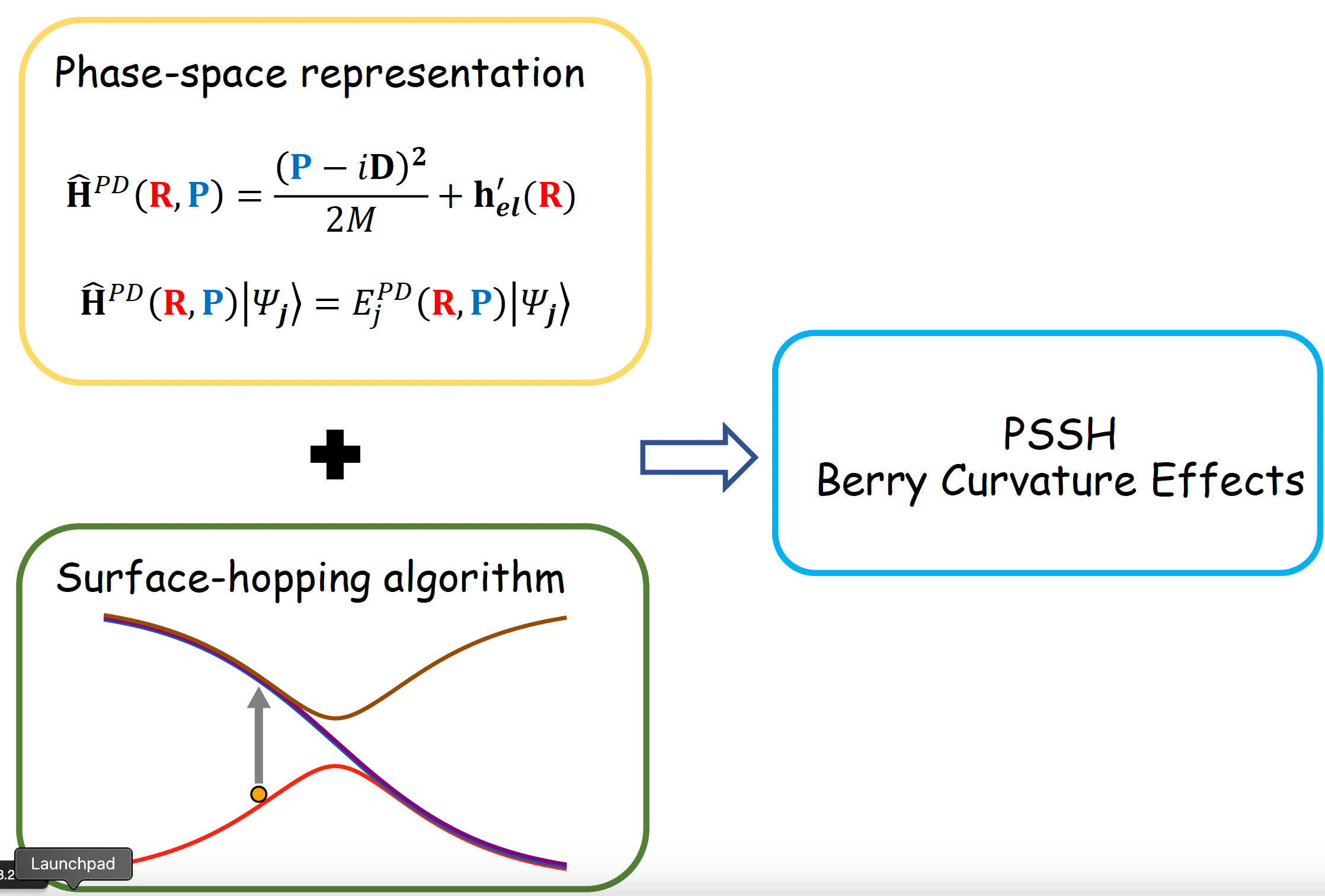
According to the standard FSSH algorithm, after a hop, trajectory’s momentum needs to be rescaled along the direction of non-adiabatic coupling to conserve the total energy. However, when spin-related couplings (e.g., spin-orbit coupling, magnetic fields, …) are taken into account, the electronic Hamiltonian will become complex-valued. The resulting complex-valued electronic wavefunctions and non-adiabatic couplings will cause a “gauge” problem for FSSH – one cannot rescale momentum along a complex-valued direction. We have recently developed a phase-space surface hopping (PSSH) algorithm that overcomes the gauge problem and shows much better results comparing to the standard FSSH in model systems.
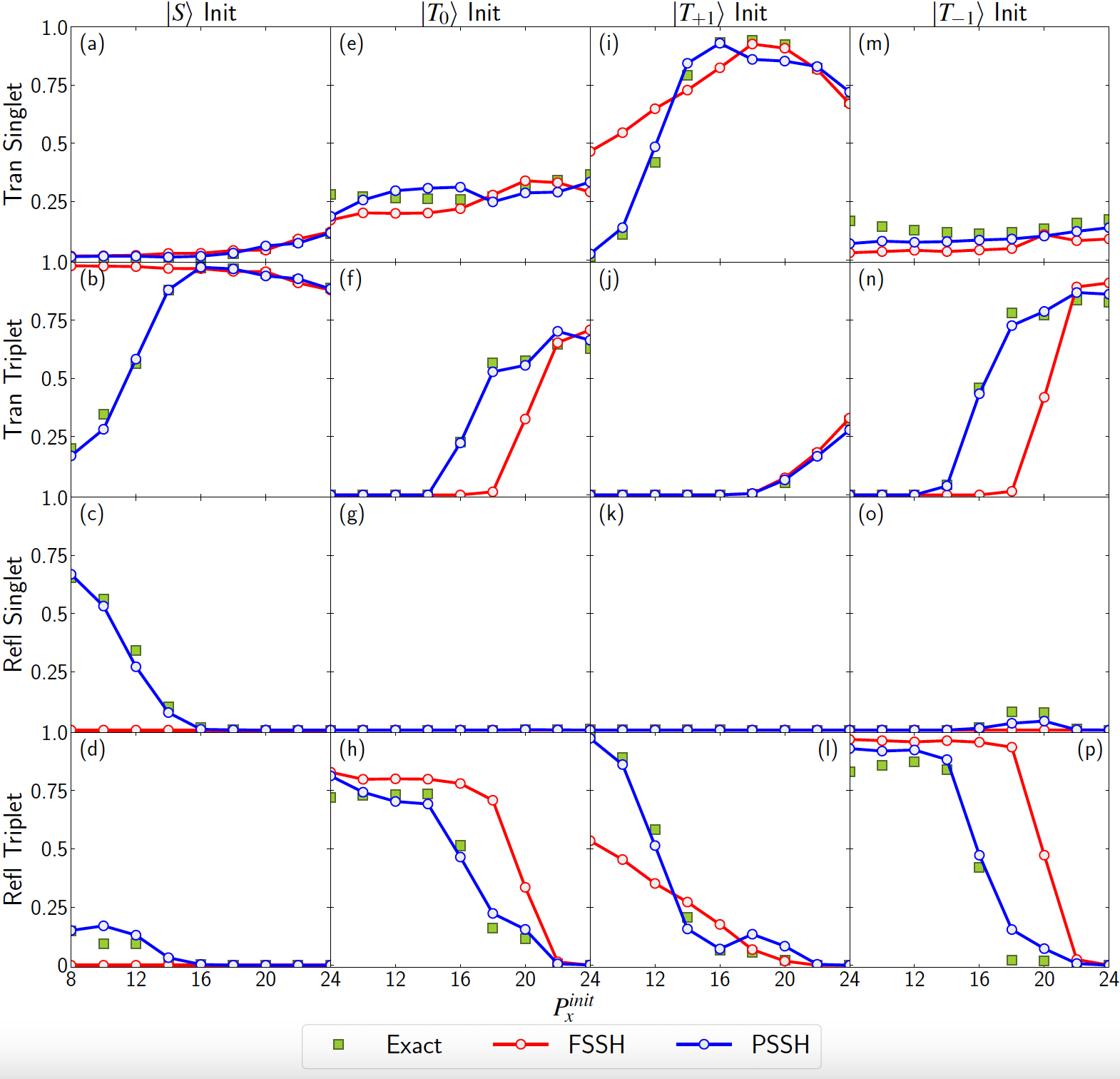
The basic idea of PSSH is to first find an optimal pre-conditioned basis and diagonalize the total Hamiltonian (nuclear + electronic) under that basis. The energy eigensurface and eigenfunctions will depend on both nuclear position and momentum.